中国眼科龙头—爱尔眼科：为什么业绩年年增长，股价却连续下跌？

　　炒股就看金麒麟分析师研报，权威，专业，及时，全面，助您挖掘潜力主题机会！

　　来源：黑马财经圈

　　爱尔眼科

　　应很多粉丝朋友的要求，让我来聊一聊爱尔眼科这家公司

　　因为很多朋友跟我说，之前看到爱尔眼科跌下来了，发现业绩不错，净利润年年增长，估值也比较低！

　　按照惯性的思维，这种公司回调往往是上车的机会，所以就越跌越买

　　但是没想到这几年越套越深！

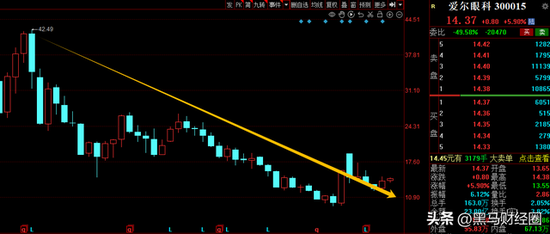
　　如果从21年高点42块算起的话，爱尔眼科最低跌到9块，最大跌幅一度超过80%，人均亏损超过200万！

　　他们想不明白，爱尔眼科为什么业绩那么好，股价却走成这样？

　　所以，这期不讲半导体芯片公司，专门来聊聊这个这只曾经的浓眉大眼的白马股！

　　看看它在这几年到底发生了什么！

　　还有，普通者应该吸取怎样的教训，以后才能避免这种情况的发生！

　　30多倍PE，1200亿市值的爱尔眼科，还有没有投资的价值？

　　继续来聊聊这几个问题！

　　刷到我的朋友，不妨点个免费的关注，后面我每天都会给大家聊透一家A股的上市公司带你们看懂大资金背后的行为逻辑！

　　先来简单了解一下，爱尔眼科是做什么的；

　　爱尔眼科是一家全球性的眼科连锁医疗机构，成立于2002年，2009年在创业板上市，公司主营业务包括屈光手术，视光服务、白内障手术、眼前段手术等等！

　　其中，屈光手术就是我们常说的近视、远视、散光等视力矫正手术，针对青少年群体！

　　而视光服务包括医学验光、配镜以及角膜塑形镜等特殊镜片的验配，也是针对青少年，白内障手术主要针对老年人！

　　了解了爱尔眼科是做什么的之后，我们回到刚开始的那个问题！

　　为什么净利润年年增长，股价还跌成这样！

　　因为资金提前预判了爱尔眼科的增长预期，即将不在了！

　　首先，爱尔眼科的外延式并购带来的高增长，在这几年已经不太管用了！

　　因为这几年国内适合开眼科医院的地方，已经被爱尔眼科跑马圈地给开发完了

　　我举个简单的例子，10年前，爱尔眼科只开了48家店，全国293个地级市，平均4座城市1家店；

　　而到了24年前三季度，加上并购和新建的，爱尔眼科的门店基本去到了780家，相当于一个地级市接近3家店！

　　对于眼科这个赛道来说，已经快要饱和了！

　　爱尔眼科的成长路径是是‘内生培育+外延并购’双轮驱动，虽然说这个模式创造了医疗行业的资本扩张奇迹，但也埋下了结构性风险！

　　例如爱尔眼科前三季度累计87亿元商誉，占总资产26.3%，一旦单店盈利下滑将引发连锁减值！

　　一般情况下，商誉占总资产的比例过高可能意味着公司进行了大量溢价收购

　　如果商誉占总资产比例超过30%，就是比较高的水平，说明这家公司依赖并购扩张，且未来可能面临较大的减值压力。

　　其次是，爱尔眼科的核心收入叫做屈光项目、还有视光服务，这两个业务收入占比超过60%，服务的对象主要是青少年！

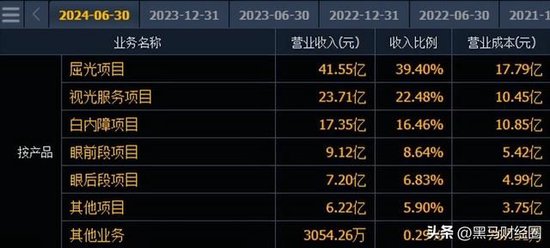
　　自从2017年以来，我们的出生率就持续下滑，2023年达到历史最低点6.34‰，目前出生率还是处在很低的水平！

　　而且，新生儿人口也逐年下降，17年全国的新生儿人口还有1700万，23年差点跌破了900万，接近腰斩！

　　细心的朋友可以发现，这两年经常可以看到一些幼儿园、小学因为招不到学生而倒闭了！

　　以前我们读小学的时候，一个班接近90个人，现在有些地方的小学，凑个50人都费劲！

　　新生儿的大幅减少，就意味着爱尔眼科未来的潜在客户基数也会将大幅减少，这是可以预见的，是堪忧的！

　　而聪明资金都是先知先觉，早在爱尔眼科股价巅峰的时候就开始出逃！

　　而没有看清楚本质的散户，看到爱尔眼科股价跌下来了，看到净利润还在增长，估值越来越低，以为是回调上车的，其实这就是很典型的价值投资陷阱！

　　再来聊聊估值这块，目前爱尔眼科估值是35倍！

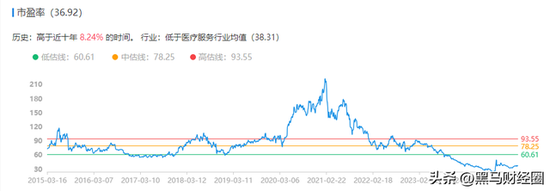
　　估值都是建立在业绩增速上的，一般，业绩增速高，估值高点也可以通过业绩去消化！

　　比如业绩增速高达70%的那种，估值我们也就可以给到60倍甚至100倍；

　　但是当业绩增速放缓，甚至未来业绩还会下滑的那种，20倍到顶！

　　而且就算是20倍，你买一个业绩不增长的公司图什么？

　　更何况现在爱尔眼科跌了这么多之后，现在估值还在30倍以上！

　　如果你已经看到了这里，我想你已经明白了我对爱尔眼科的价值判断！