借贷宝第二次被央视315曝光:利率高达2234.69%
- 体育资讯
- 2025-03-15 23:57:06
- 14
- 更新:2025-03-15 23:57:06
专题:2025年金融315投诉曝光台
继2016年央视点名借贷宝裸条事件后8年,借贷宝在上央视315晚会。
据央视315晚会报道,借贷宝、人人信等电子签平台上电子借条几乎不监管,利率竟然可以高达2234.69%。
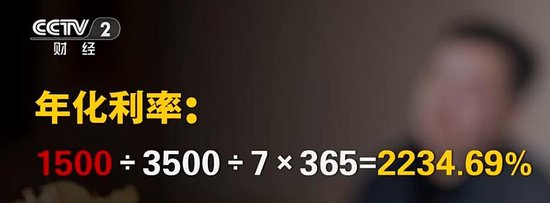
借贷宝官网的最新数据显示,目前已经9年稳健运营,有1.4亿注册用户,1.1亿笔登记借条,1000万人成功借款,但该信息已经许久并未更新了。
官网显示,借贷宝与绝大部分包括五大行、全国制股份行等都有合作。

最新工商信息显示,借贷宝主体人人行科技股份有限公司,成立于2014年12月22日,法定代表人为王璐,注册资本是30亿人民币,控股股东为借贷宝(香港)有限公司。
此前借贷宝官网介绍,借贷宝是由国内私募机构九鼎控股倾力打造的互联网社交金融平台。公司的核心团队皆来自国内外知名金融机构、法律机构,以及百度、阿里、腾讯等知名互联网公司。
公开资料显示,九鼎控股是国内金融控股集团,旗下九鼎集团(股票代码:430719)、九鼎投资(股票代码:600053)是国内综合性资产管理机构。九鼎旗下还拥有多家金融机构,包括九州证券、九泰基金、富通保险(Ageas Asia Holdings Limited)、九信金融、九州期货、中捷保险经纪、支付公司九派支付等,曾入股梧桐理财、团贷网等多个P2P平台。
2016年底,央视《焦点访谈》曝光一家名叫借贷宝的平台上,不少人都存在着从平台上借入资金的情况,少的几十万元,多的甚至一、两百万元。而为了防范在同一平台借入资金过多导致的坏账风险,8月24日颁布的暂行办法明确规定:“同一自然人在同一网络借贷信息中介机构平台的借款余额上限不超过人民币20万元”,借贷宝明显超越这条红线。记者来到了借贷宝公司,接待人员说,记者了解到的情况确实存在,但暂行办法对公司没有约束力。
随后事件持续发酵和升级。
遭央视曝光后,11月25日,借贷宝的“赚利差”项目正式下线;11月29日,媒体曝光借贷宝上出现网络消费陷阱,有用户未借款却先负债;11月30日晚,有网友曝光借贷宝女大学生借款裸条照片被泄露,大小达到10G。对此,借贷宝回应称借贷宝是合法合规的网络直接借贷平台,平台上从未产生、储存过任何“裸条”照片。
裸条在彼时是借贷宝上公开的秘密,也让借贷宝持续站上风口浪尖。
沉寂数年后的2019年,人人行副总裁曾军在接受媒体采访时表示,公司旗下借贷宝已做好上市前的一切准备,正等待合适的时机,预计最快将在年内赴港上市。
不过此后,借贷宝却没有进一步的上市动作,反而卷入多起“套路贷”案件。
2021年1月,红山区公安分局成功抓获“套路贷”诈骗案犯罪嫌疑人6人,教育惩戒12人。案件中,犯罪嫌疑人利用“借贷宝”等APP业务员的名义向被害人进行放贷,贷款利息均为30%以上,超过还款时间就会每天按照利息的10%或者借款金额的10%计算。
2021年7月,福建宁德公安机关成功打掉一个主要从事网络套路贷的有组织犯罪组织,抓获犯罪嫌疑人20余人,破获刑事案件20余起,查扣涉案财产2亿元,此案犯罪嫌疑人柯某锋等人在福州市成立无网络贷款资质的“佰仟借条”公司,利用“借贷宝”平台,通过制造虚假流水、恶意垒高债务、软暴力催收等手段,长期有组织地实施网络套路贷违法犯罪活动。
2023年2月,四川内江市公安局披露,有组织自2017年12月至2020年6月期间,分别利用“借贷宝”等平台和“恒丰e贷”等APP,虚增与“砍头息”金额一致的“保证金”,累计向全国31省市大量受害人实施“套路贷”诈骗,非法获利上亿元。
半年前,蓝鲸财经曾独家报道借贷宝再度重启贷超流量业务,主体是重庆的小贷。
蓝鲸新闻发现,借贷宝上线的贷超流量业务在其平台中被称为,5万额度以下的“中小额贷款直接找机构”以及5万额度以上的“大额借款找助贷机构”。
蓝鲸新闻调查发现,借贷宝平台显示的“精选贷款推荐”后展示了三家知名银行标识,并显示最高可借20万元,年利率为7.2%-24%。然而,点进申请界面后,所展示的贷款机构并不是上述三家银行,而是贷款平台小美易融、吉用花等。
比如其中的吉用花的主体为深圳市中安信业小额贷款有限公司。7月10日,深圳市地方金融管理局发布关于“空壳”小额贷款公司的公告显示,深圳市中安信业小额贷款有限公司因长期无正当理由自行停业被列为“空壳”小额贷款公司。
此外,借贷宝提供的5万额度以上的“大额借款找助贷机构”服务,则是将用户导流至本地贷款中介。先由中介筛选出三家贷款机构,之后用户再自行从中三选一。