吃喝板块继续反攻,食品ETF(515710)盘中上探1.3%!机构:食品饮料等领域有望提振
- 互联网
- 2025-03-09 21:51:02
- 18
- 更新:2025-03-09 21:51:02
7日午后,吃喝板块午后吹响反攻号角,白酒领衔上攻!截至收盘,迎驾贡酒飙涨5.45%,今世缘、泸州老窖双双大涨超4%,水井坊、五粮液、山西汾酒收涨超2%,贵州茅台、洋河股份等白酒龙头亦小幅收红。
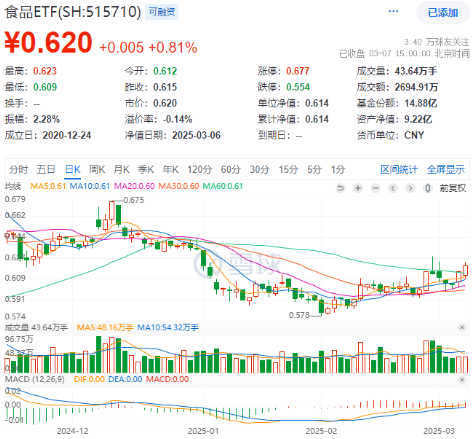
场内热门ETF方面,反映吃喝板块整体走势的食品ETF(515710)午后直线拉升,盘中场内价格涨幅一度达到1.3%,截至收盘,涨0.81%。
节后,白酒板块屡屡上攻,中信证券研报表示,当前白酒行业正处于过去三十年以来第三轮大周期的筑底阶段,虽然短期内行业基本面仍需继续承压,走出底部的实质性拐点仍须观察,但投资端伴随政策信号、经济修复预期上升、终端需求企稳等信号推动情绪回暖,预计白酒行业资本市场表现或将先于产业表现迎来向上周期,而在白酒产业新一轮上升期中,以消费者培育为根基、品牌力持续提升的头部名酒企业会有更好表现。
消息面上,众多白酒企业纷纷加强市值管理。3月5日晚间,五粮液发布了市值管理制度,公司董事会是市值管理工作的领导机构,高级管理人员协同参与市值管理工作,董事会办公室是市值管理的具体执行部门,职能部门及子公司应当全力支持与配合。贵州茅台也在3月4日晚间发布了股票回购进展,截至2025年2月底,已累计回购股份82.22万股,已支付的总金额近12亿元(不含交易费用)。
而随着龙头酒企对市值管理的重视程度不断加强,投资者对于板块信心有望得到进一步提振,白酒板块股价企稳回升的态势有望得到进一步稳固。
从估值方面来看,Wind数据显示,截至6日收盘,食品ETF(515710)标的指数细分食品指数市盈率为20.25倍,位于近10年来4.12%分位点的低位,中长期配置性价比凸显。

展望吃喝板块后市,开源证券指出,低估值、基本面逐步改善的食品饮料有望重新获得资金青睐。同时观察地产数据也有转暖迹象,二手房成交面积升温,价格降幅收窄,地产有逐渐企稳迹象,或为消费复苏奠定基础。当前提振消费是重要会议要务,2025年政策大概率为宽松基调,叠加如消费券等地方财政刺激,外部环境或将进一步促进消费复苏进程。食品饮料板块有望获益。
国泰君安表示,重要报告将“大力提振消费、提高投资效益,全方位扩大国内需求”作为2025年工作任务的第一条,提出“加快补上内需特别是消费短板,使内需成为拉动经济增长的主动力和稳定锚”,体现出对消费和内需的极大重视。其认为,随着稳就业、增收入、促生育、落实休假和补贴等措施推出,服务消费、情绪消费等领域增长潜力有望持续释放,预计食品饮料等领域大众消费有望提振。
一键配置吃喝板块核心资产,重点关注食品ETF(515710)。根据中证指数公司统计,食品ETF(515710)跟踪中证细分食品饮料产业主题指数,约6成仓位布局高端、次高端白酒龙头股,近4成仓位兼顾饮料乳品、调味、啤酒等细分板块龙头股,前十权重股包括“茅五泸汾洋”、伊利股份、海天味业等。场外投资者亦可通过食品ETF联接基金(A类012548/C类012549)对吃喝板块核心资产进行布局。
图片、数据来源:沪深交易所、Wind等,截至2025.3.7。注:“全市场首只”是指首只跟踪创业板人工智能指数的ETF。
风险提示:食品ETF被动跟踪中证细分食品饮料产业主题指数,该指数基日为2004.12.31,发布于2012.4.11。指数成份股构成根据该指数编制规则适时调整,其回测历史业绩不预示指数未来表现。文中提及个股仅为指数成份股客观展示列举,不作为任何个股推荐,不代表基金管理人和基金投资方向。任何在本文出现的信息(包括但不限于个股、评论、预测、图表、指标、理论、任何形式的表述等)均只作为参考,投资人须对任何自主决定的投资行为负责。另,本文中的任何观点、分析及预测不构成对阅读者任何形式的投资建议,亦不对因使用本文内容所引发的直接或间接损失负任何责任。投资人应当认真阅读《基金合同》、《招募说明书》、《基金产品资料概要》等基金法律文件,了解基金的风险收益特征,选择与自身风险承受能力相适应的产品。基金的过往业绩并不预示其未来表现,基金管理人管理的其他基金的业绩并不构成基金业绩表现的保证。根据基金管理人的评估,食品ETF风险等级为R3-中风险,适宜平衡型(C3)及以上的投资者,适当性匹配意见请以销售机构为准。销售机构(包括基金管理人直销机构和其他销售机构)根据相关法律法规对以上基金进行风险评价,投资者应及时关注基金管理人出具的适当性意见,各销售机构关于适当性的意见不必然一致,且基金销售机构所出具的基金产品风险等级评价结果不得低于基金管理人作出的风险等级评价结果。基金合同中关于基金风险收益特征与基金风险等级因考虑因素不同而存在差异。投资者应了解基金的风险收益情况,结合自身投资目的、期限、投资经验及风险承受能力谨慎选择基金产品并自行承担风险。中国证监会对以上基金的注册,并不表明其对本基金的投资价值、市场前景和收益做出实质性判断或保证。基金投资须谨慎。